DAYV: MOVIMIENTO PARABOLICO

MOVIMIENTO PARABÓLICO

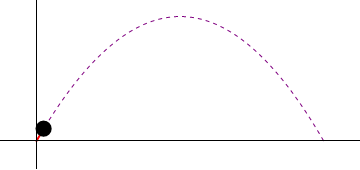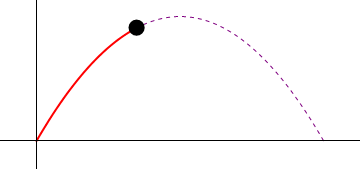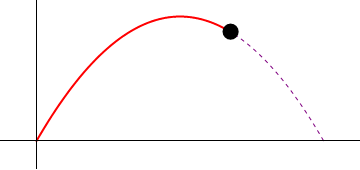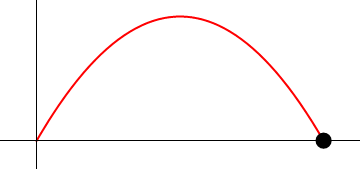
Supóngase el movimiento de un proyectil que se caracteriza por poseer una aceleración constante
$\vec{a}(t)=-g\vec{k}$ una posición inicial nula ( $\vec{r}_0=\vec{0}$ ) y una velocidad inicial que forma un ángulo

α

con la horizontal y tiene rapidez inicial

v 0

Determine el vector de posición, la velocidad y la aceleración en cada instante.
Calcule la celeridad y el vector tangente en el instante inicial, en el instante en que se encuentra a mayor altura y en el momento en que vuelve a impactar con el suelo.
Halle la aceleración tangencial y la aceleración normal, así como el vector unitario normal en los tres instantes anteriores.
Calcule el radio de curvatura y el centro de curvatura en el punto más alto de la trayectoria.
Para este mismo punto, halle las componentes intrínsecas de la velocidad y la aceleración, así como el radio de curvatura, si $\alpha = 45^\circ$ , $v_0=25.0\,\mathrm{m}/\mathrm{s}$ y $g=9.81\,\mathrm{m}/\mathrm{s}^2$ .

2 Posición, velocidad y aceleración

Al ser la aceleración constante, la integración es inmediata:
$\vec{r}(t) = \vec{r}_0 + \vec{v}_0t+\frac{1}{2}\vec{g}t^2$ La posición inicial, según nos indica el enunciado, es nula
$\vec{r}_0 =\vec{0}$ mientras que la velocidad inicial posee módulo

v 0

y forma un ángulo

α

con la horizontal
$\vec{v}_0 = v_0\cos(\alpha)\vec{\imath}+v_0\,\mathrm{sen}(\alpha)\vec{k}$ lo que nos da el vector de posición en cada instante
$\vec{r}=(v_0\cos\alpha)t\vec{\imath}+\left((v_0\,\mathrm{sen}\,\alpha)t-\frac{1}{2}gt^2\right)\vec{k}$ Derivando el vector de posición respecto al tiempo obtenemos la velocidad intantánea
$\vec{v}=\dot{\vec{r}}=(v_0\cos\alpha)\vec{\imath}+\left(v_0\,\mathrm{sen}\,\alpha-gt\right)\vec{k}$ La velocidad de avance horizontal permanece constante, mientras que la vertical varía linealmente con el tiempo. Comienza siendo positiva, se anula en el punto más alto, y a partir de ahí es negativa.
Para la aceleración, derivamos la velocidad instantánea respecto al tiempo y comprobamos que, tal como indica el enunciado, es constante
$\vec{a}=\dot{\vec{v}}=-g\vec{k}$

Posición	Velocidad	Aceleración

3 Celeridad y vector tangente

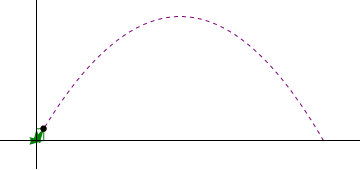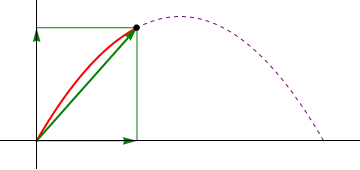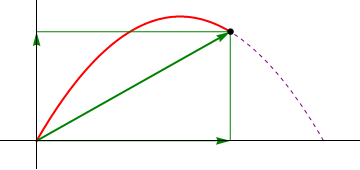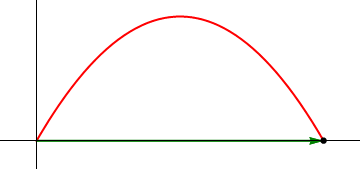
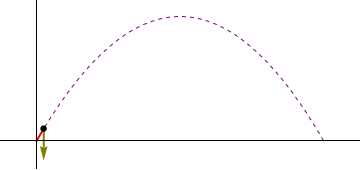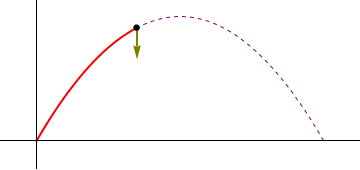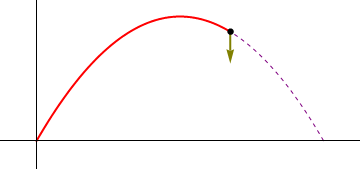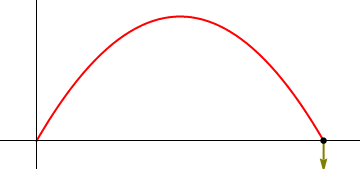
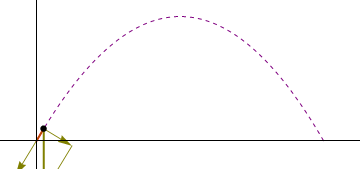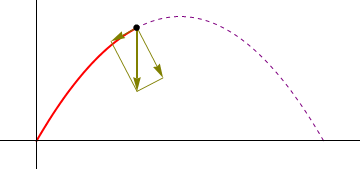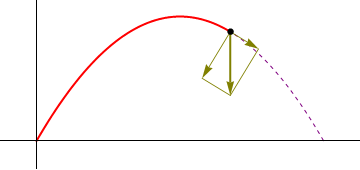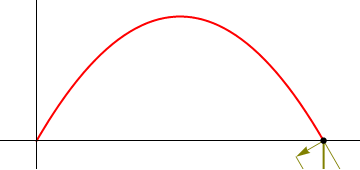
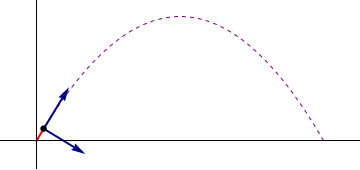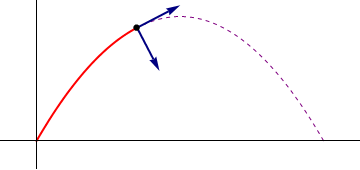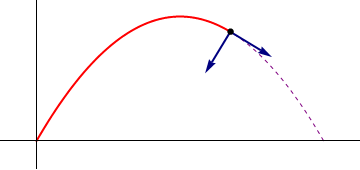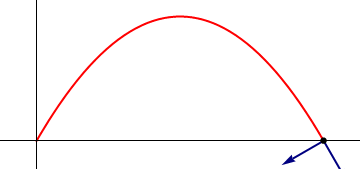
Los tres instantes en que debemos calcular las diferentes magnitudes son:

Instante inicial: La partícula despega en $t 1 = 0$ .
Punto de máxima altura: La máxima altura se alcanza cuando $z$ tiene un máximo, esto es, cuando la componente $z$ de la velocidad es nula

$0 = \frac{\mathrm{d}z}{\mathrm{d}t}=v_z = v_0\,\mathrm{sen}\,\alpha-gt$ $\Rightarrow$ $t_2 = \frac{v_0\,\mathrm{sen}\,\alpha}{g}$

Punto de impacto: el proyectil choca de nuevo con el suelo cuando $z = 0$ , lo que ocurre en el instante

$(v_0\,\mathrm{sen}\,\alpha)t-\frac{1}{2}gt^2=0$ $\Rightarrow$ $t_3=\frac{2v_0\,\mathrm{sen}\,\alpha}{g} = 2t_2$ El tiempo que tarda en impactar es el doble del que tarda en llegar al punto más alto, como corresponde a que el movimiento es simétrico respecto a este punto, que es el vértice de la parábola.
La posiciones, velocidades y aceleraciones, en estos tres instantes las hallamos sustituyendo en las ecuaciones anteriores

Instante inicial

$\vec{r}_1=\vec{0}$ $\vec{v}_1=v_0\cos\alpha\vec{\imath}+v_0\,\mathrm{sen}\,\alpha\vec{k}$ $\vec{a}_1=-g\vec{k}$

Punto de máxima altura

$\vec{r}_2=\frac{v_0^2\,\mathrm{sen}\,\alpha\cos\alpha}{g}\vec{\imath}+\frac{v_0^2\,\mathrm{sen}^2\alpha}{2g}\vec{k}$ $\vec{v}_2=v_0\cos\alpha\vec{\imath}$ $\vec{a}_2=-g\vec{k}$

Punto de impacto

$\vec{r}_3=\frac{2v_0^2\,\mathrm{sen}\,\alpha\cos\alpha}{g}\vec{\imath}$ $\vec{v}_3=v_0\cos\alpha\vec{\imath}-v_0\,\mathrm{sen}\,\alpha\vec{k}$ $\vec{a}_3=-g\vec{k}$

3.1 Celeridad

la celeridad es el módulo de la velocidad. Para los tres instantes anteriores vale

Instante inicial

$v_1 = |\vec{v}_1| = \sqrt{v_0^2\cos^2\alpha+v_0^2\,\mathrm{sen}^2\alpha}=v_0$

Punto de máxima altura

$v_2 = v_0\cos\alpha\,$

Punto de impacto

$v_3 = |\vec{v}_3| = \sqrt{v_0^2\cos^2\alpha+v_0^2\,\mathrm{sen}^2\alpha}=v_0$

3.2 Vector tangente

Obtenemos el vector tangente en cada uno de los instantes dividiendo la velocidad por su módulo

Instante inicial

$\vec{T}_1 = \frac{\vec{v}_1}{v_1}=\cos\alpha\vec{\imath}+\,\mathrm{sen}\,\alpha\vec{k}$

Punto de máxima altura

$\vec{T}_2 = \frac{\vec{v}_2}{v_2}=\vec{\imath}$

Punto de impacto

$\vec{T}_3 = \frac{\vec{v}_3}{v_3}=\cos\alpha\vec{\imath}-\,\mathrm{sen}\,\alpha\vec{k}$

4 Componentes intrínsecas de la aceleración

4.1 Aceleración tangencial

Obtenemos la componente tangencial de la aceleración proyectando sobre el vector tangente
$a_t = \vec{a}\cdot\vec{T}=\frac{\vec{a}\cdot\vec{v}}{v}$ Para los tres instantes señalados es

Instante inicial

$a_{t1}=-g\,\mathrm{sen}\,\alpha$

Punto de máxima altura

$a_{t2}=0\,$

Punto de impacto

$a_{t3}=g\,\mathrm{sen}\,\alpha$ Vemos que, aunque la aceleración es constante, la aceleración tangencial no lo es. En el instante inicial es negativa, lo que indica que la partícula se está frenando. La celeridad alcanza un mínimo en el vértice de la parábola y a partir de ahí comienza a aumentar. En el punto de impacto la aceleración tangencial es positiva, lo que indica que la partícula se mueve cada vez más rápido.
En forma vectorial la aceleración tangencial es
$\vec{a}_t = (\vec{a}\cdot\vec{T})\vec{T}=\frac{(\vec{a}\cdot\vec{v})\vec{v}}{v^2}$ que nos da

Instante inicial

$\vec{a}_{t1}=-g\,\mathrm{sen}\,\alpha(\cos\alpha\vec{\imath}+\,\mathrm{sen}\,\alpha\vec{k})$

Punto de máxima altura

$\vec{a}_{t2}=\vec{0}\,$

Punto de impacto

$\vec{a}_{t3}=g\,\mathrm{sen}\,\alpha(\cos\alpha\vec{\imath}-\,\mathrm{sen}\,\alpha\vec{k})$

4.2 Aceleración normal

Una vez que tenemos la aceleración tangencial en cada uno de los tres puntos calculamos la aceleración normal restando
$\vec{a}_n = \vec{a}-\vec{a}_t$ Lo que nos da, en cada uno de los tres casos que estamos considerando

Instante inicial

$\vec{a}_{n1}=-g\vec{k}+g\,\mathrm{sen}\,\alpha(\cos\alpha\vec{\imath}+\,\mathrm{sen}\,\alpha\vec{k})=g\cos\alpha(\mathrm{sen}\,\alpha\vec{\imath}-\cos\alpha\vec{k})$

Punto de máxima altura

$\vec{a}_{n2}=-g\vec{k}$

Punto de impacto

$\vec{a}_{n3}=-g\vec{k}-g\,\mathrm{sen}\,\alpha(\cos\alpha\vec{\imath}-\,\mathrm{sen}\,\alpha\vec{k})=g\cos\alpha(-\mathrm{sen}\,\alpha\vec{\imath}-\cos\alpha\vec{k})$ En módulo, estas tres aceleraciones normales valen

Instante inicial

$a_{n1}=g\cos\alpha\,$

Punto de máxima altura

$a_{n2}=g\,$

Punto de impacto

$a_{n3}=g\cos\alpha\,$

4.3 Vector normal

El vector unitario normal lo hallamos dividiendo la aceleración normal por su módulo
$\vec{N}=\frac{\vec{a}_n}{a_n}$ y nos da

Instante inicial

$\vec{N}_{1}=\mathrm{sen}\,\alpha\vec{\imath}-\cos\alpha\vec{k}$

Punto de máxima altura

$\vec{N}_{2}=-\vec{k}$

Punto de impacto

$\vec{N}_{3}=-\mathrm{sen}\,\alpha\vec{\imath}-\cos\alpha\vec{k}$ Vemos que en todos los casos el vector normal apunta hacia el interior de la curva (entendiendo por interior el lado hacia el que se curva). Es inmediato comprobar que estos vectores son ortogonales a los vectores tangentes en cada caso.
Podemos hallar el vector binormal en cada uno de los tres instantes, multiplicando el vector tangente por el normal
$\vec{B}=\vec{T}\times\vec{N}$ que, en los tres casos da
$\vec{B}_1=\vec{B}_2=\vec{B}_3=\vec{\jmath}$ lo que corresponde al hecho de que estamos ante una trayectoria plana, que tiene, por tanto, un vector binormal constante.

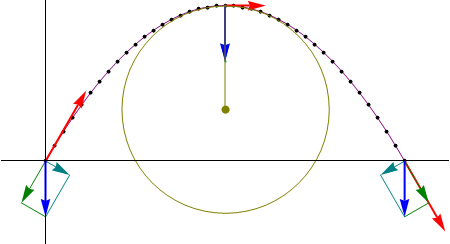
5 Radio y centro de curvatura

5.1 Radio de curvatura

Una vez que tenemos la aceleración normal y la celeridad hallamos el radio de curvatura como
$R=\frac{v^2}{a_n}$ Sustituyendo tenemos, para el punto de máxima altura
$R=\frac{v_0^2\cos^2\alpha}{g}$ El centro de curvatura lo obtenemos a partir de la posición de la partícula, el radio de curvatura y del vector normal
$\vec{r}_c = \vec{r}+R\vec{N}$ lo que nos da, para este punto
$\vec{r}_{c}=\frac{v_0^2\,\mathrm{sen}\,\alpha\cos\alpha}{g}\vec{\imath}+\frac{v_0^2(\mathrm{sen}^2\alpha-2\cos^2\alpha)}{2g}\vec{k}$

6 Valores numéricos

La componente tangencial de la velocidad es igual a su módulo, que para el vértice de la parábola vale
$v = v_0\cos\alpha = \frac{25.0}{\sqrt{2}}\,\frac{\mathrm{m}}{\mathrm{s}} = 17.7\,\frac{\mathrm{m}}{\mathrm{s}}$ En el vértice de la parábola, según hemos visto, la aceleración es puramente normal, por lo que
$a_t = 0\,$ $a_n = 9.81\,\frac{\mathrm{m}}{\mathrm{s}^2}$ El radio de curvatura en este punto vale
$R = \frac{v^2}{a_n} = 31.9\,\mathrm{m}$ Por último, el centro de curvatura lo obtenemos a partir de la posición del vértice de la parábola y el radio de curvatura. La partícula alcanza el vértice en el instante en que velocidad vertical se anula
$t_2 = \frac{v_0\,\mathrm{sen}\,\alpha}{g} = 1.80\,\mathrm{s}$ La posición en ese momento es
$\vec{r}_2 = (31.9\,\vec{\imath}+15.9\,\vec{k})\,\mathrm{m}$ Sumando a este punto el radio de curvatura multiplicado por el vector normal
$\vec{r}_c = \vec{r}_2+R\vec{N}=(31.9\,\vec{\imath}-15.9\,\vec{k})\,\mathrm{m}$ El hecho de que resulte el simétrico es consecuencia de que el ángulo inicial sea de 45°. Para otros ángulos no se produce esta situación.

DAYV

viernes, 5 de abril de 2013

MOVIMIENTO PARABOLICO